Making Sense of Numbing Numbers

As if it weren't hard enough to be a voter in 2012, what with negative advertising screaming in our ears while we try to sort through claims and counter claims and counter-counter claims. And now, what? Math! You gotta be kidding me!

You can't look at a newspaper, change the channel or even check your Twitter without having to grapple with numbers, numbers and more numbers. If 47% of Americans don't pay federal income taxes, then 53% do, but what's the ratio between income taxes and payroll taxes or the percentage of non-payers who are in combat zones, and just what's fair, anyway? The numbers just keep coming. It's enough to make your head hurt.

There are plenty of folks -- well-intentioned and otherwise -- trying to analyze, explain and put the perfect spin on Mitt Romney's controversial comments at that fundraiser in Florida. We'd like to offer some help on a related issue by dusting off a piece on math anxiety that we published back in 1990, a time at which fully 45.9% of Americans living today had not yet been born. One telling line from the story: "You can use data to prove almost anything, partly because people too readily believe 'facts' presented with numbers." (By the way, we just made up that statistic about the percentage of people born since the story was originally published.)

From just $107.88 $24.99 for Kiplinger Personal Finance

Become a smarter, better informed investor. Subscribe from just $107.88 $24.99, plus get up to 4 Special Issues

CLICK FOR FREE ISSUE

Sign up for Kiplinger’s Free Newsletters

Profit and prosper with the best of expert advice on investing, taxes, retirement, personal finance and more - straight to your e-mail.

Profit and prosper with the best of expert advice - straight to your e-mail.

Sign up

The story holds up extremely well after more than two decades, but some of the numbers might seem startling. Just remember that back in 1990, 30-year home mortgages were averaging over 10%, money market mutual funds were yielding over 7.5%, the annual inflation rate was 5.4% and the Dow Jones Industrial Average closed the year at 2634.

From Kiplinger's Personal Finance magazine, August 1990:

When Numbers Make You Numb

Does the term "math anxiety" barely begin to describe your fear of numbers? You're nodding your head, but don't turn the page – there's only one formula in this article, and you can avert your eyes when you come to it. You won't emerge a math whiz, but you will sharpen what Temple University math professor John Allen Paulos calls the "rough, numerical horse sense" needed to get along in today's world.

Solomon Garfunkel, executive director of the Consortium for Mathematics and Its Applicators, worries that people too often benignly accept what they're told when math is involved because they don't trust themselves to know better. "That can get very scary," he says. It makes people susceptible to inferior investments and questionable proposals.Protecting yourself doesn't mean carrying a loaded calculator. More often than not, you need know only what questions to ask, not how to decipher the answers.

1. Compound versus simple

People simply don't comprehend the power of compounding, laments Garfunkel. "As much as it is the basis of all financial computation, people still don't understand the effects of compounding on both savings and debt."

On the savings side, the easiest way to think of compounding is that you earn interest on interest as well as on your original investment. Invest $100 at 10% compounded annually and at the end of the first year you have $110 ($100 plus $10). That $110 earns interest the second year, so you end the year with $121 ($110 plus $11). And so on. By contrast, with simple interest you earn only on your original investment. Thus, you end year one with $110, year two with $120 and so forth, adding just $10 each year.

It's also easy to underestimate the power of compounding. At low interest rates and over short periods of time, the effect is modest. Then it snowballs. The longer the earnings compound, the faster the growth accelerates.

Imagine two checkerboards, with the squares representing 64 years. Put 2 cents on the lower left-hand square of each board and assume you'll earn 100% interest each year, with larger and larger piles of money accumulating on each square as you go along.

On one checkerboard, you earn simple interest, adding 2 cents to your booty on each successive square: 2 cents, 4 cents, 6 cents, 8 cents and so on. At the 64th square you have $1.28. On the other board, your 100% interest compounds annually: 2 cents, 4 cents, 8 cents, 16 cents, etc. How much do you have by the time you reach the 64th square? Would you believe $184 quadrillion? That's $184 followed by 15 zeros. In just the final year, the interest amounts to $92,000,000,000,000,000. Such is the power of compounding.

You don't have to know how to calculate that phenomenal figure to realize that compounding is a key to investment performance. Consider this real-world example: An investment is ballyhooed for having generated an average annual return of 20% a year for ten years. In other words, it increased in value by 200% over the decade. Or, put another way, it returned a simple noncompounded annual yield of 20%.

But a 200% return over ten years translates to an 11.6% compounded annual return. That's not bad, but it's anemic beside the 20% "average" return being hyped. With a financial calculator, you can make quick work of translating average returns to annual yields.

Even without a calculator, you can protect yourself from being bamboozled by asking that all rates be translated to effective annual yields and that multiyear returns reflect annual compounding.

[page break]

Page 2 of 3

2. High cost of higher interest

Compounding works against you when it comes to debt. Lynn Steen, a math professor at St. Olaf College, in Northfield, Minn., warns that lack of understanding here can cause havoc when variable-interest-rate loans are involved. Although a one point increase in interest rates may appear modest, Steen notes that it can have a major impact on a person's ability to repay a loan.

Consider, for example, how the payoff period stretches out on an $85,000 mortgage, assuming that monthly payments remain unchanged at $800 as the interest rate moves up from 10.85%.

At 10.85%, the mortgage is paid off in the traditional 30 years. If the rate rises to 11%, you'll be paying that $800 a month for more than three extra years. And if it goes to 11.3%, hold on! You'll be paying $800 for the rest of your life – and actually fall further and further behind – because accruing interest exceeds your payment.

Red alert: Here comes the formula, from which the squeamish may turn away:

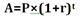
This is how you compute compound interest. A is the amount you'll have at the end of a certain amount of time. P is the beginning amount, or principal. The interest rate is r and the number of time periods for compounding is the exponent t. An exponent tells you how many times to multiply a number times itself. Thus 2 to the third power means 2×2×2.

Say you invest $1,000 in a five-year certificate of deposit that pays 10% compounding annually. Because 10% can also be written as 0.1, the formula looks like this:

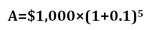
Using a calculator, you can easily find that 1.1 to the fifth power is 1.61. Because A=$1,000 × 1.61, you can figure out that your $1,000 investment will grow to $1,610 over the course of five years.

If the 10% interest were compounded monthly instead of annually, the r in this example would be 0.1÷12, or 0.0083, and the t would be 5×12, or 60. Crunching the numbers tell you that monthly compounding delivers a total of $1,645 over five years – which is $35 more than the annual compounding method.

Thankfully, this formula is built into financial calculators. But it's not terribly difficult to figure compounded interest using this formula and any calculator that figures exponents.

3. The rule of 72

This is the quick-and-easy way to estimate how long it will take you to double your money: Divide 72 by the annual return. If an investment has a 10% annual yield, for example, you'll enjoy a 100% increase in about 7.2 years (72÷10). At 8%, it takes approximately nine years (72÷8). This assumes annual compounding and once again, reinforces the power of compounding. With simple interest, it would take ten years, not 7.2, for a 10% return to double your money.

4. Percentage of what

Often enough, you read that a company boasts of a 125% increase in profits, compared with the previous year. Pretty exciting stuff, until you ask the question that should spring to your lips whenever percentages are discussed: percent of what?

If success comes after a miserable prior year, a 125% increase in profits might mean little or nothing. Companies that make "most improved" lists often are those with the most room to improve. A 125% jump in profits could actually be bad news if, say, a much greater turnabout was expected. Even if the profits are significant, you need to look beyond the numbers. For example, did the profit stem from the sale of the division that had the brightest prospects in the firm? The moral: Don't be blinded by glowing percentages.

[page break]

Page 3 of 3

5. Big numbers

"A billion here, a billion there, and pretty soon you're talking about real money." Now that the U.S. government has a multitrillion-dollar debt, that remark doesn't seem nearly as funny as it did when Sen. Everett Dirksen made it back in the '60s.

But don't let your eyes glaze over when your encounter big numbers. There's a big difference between million and billion and trillion, and it's essential that you keep it in mind. Paulos, whose book Innumeracy: Mathematical Illiteracy and its Consequences has recently been issued in paperback, illuminates the difference by noting approximately how long it takes a large number of seconds to tick by:

1 million = 11.5 days

1 billion = 31.5 years

1 trillion = 31,500 years

(By the way, this terrific book is still available.)

6. The scaling factor

Be careful when viewing graphics that help tell a story. Imagine a chart that tracks a hypothetical one-day decline in the Dow Jones industrial average, from 2700 to 2660. If it's plotted on a graph that runs from 2600 to 2700, a 40 point drop could look disastrous. But plotted on a graph that runs from 2300 to 2700, the loss would look like the result of a ho-hum trading session.

The loss is identical; the difference is the scale that's used. Always check the scale before being soothed or alarmed by what you think you see.

7. False positives

Assume that a test for a disease is 98% accurate – that is, if you have the disease, the test will be positive 98% of the time, and if you don't have it, it will be negative 98% of the time. And assuming that 1 in 200 people has the disease. After taking part in a random test, you get a call from your doctor telling you the results are positive.

"How depressed should you be?" asks Paulos, who presents this scenario. "The answer, surprisingly, is that you should be cautiously optimistic. Your change of having the disease is only about 20%."

Here's how he figures:

If 10,000 people take the test, and 1 in 200 has the disease, 49 of the 50 sick people (98%) will test positive. At the same time, 199 of the 9,950 healthy people (2%) will also test positive. So, of the 248 positive tests, 80% are false positive. "The probability that you have the disease, given that you tested positive, is only one-fifth," Paulos explains. "This is one area where innumeracy can lead to a lot of heartache."

If a test is given to someone with symptoms of a disease – rather than randomly – the odds shift dramatically. But the truth about false positives illustrates the potential danger of random detector tests, for example, or mass testing for AIDS or drug use.

8. Selective facts

You can use data to prove almost anything, partly because people too readily believe "facts" presented with numbers. Consider an article in the Wall Street Journal earlier this year by Michael Gartner, president of NBC News. Writing about a poll that showed that an increasing percentage of Americans find the press "not believable," Gartner said part of the reason is the media's use of anonymous sources. To support his theory, he noted that USA Today, which bans anonymous sources, was one of the few news outlets that improved its "highly believable" rating between 1985 and 1989.

Before giving too much credence to the connection between the ban and believability, consider other poll results Gartner didn't pass on. Even after USA Today's higher believability rating, 11 of the 17 news organizations and people in the survey were judged more believable than USA Today. And although it added two percentage points to its "highly believable" rating, USA Today also added three percentage points to its "not believable" score. Gartner could just as easily have "proved" that banning anonymous sources is a bad idea.

The better conclusion: Stay on your toes when you are bombarded with poll results.

9. What's It Worth?

You've heard it a million times: By the time you pay off a 30-year mortgage, you will have paid three times more than the purchase price of the house. Seldom stated, though, is that the final monthly payment 30 years from now will be worth just a fraction of what it's worth today.

For example, a $100,000, 30-year mortgage at 10% requires monthly payments of $878. Over 30 years, sure enough, you'll pay a total of $316,000. But what's that last payment worth in today's dollars? If you assume an 8% annual return (and ignore taxes), you need set aside only about $87 today to have the $878 in the year 2020. Another way to look at this is to ask how much you would have to pay for an 8% annuity that would pay $878 a month for the next 30 years. The cost today for a stream of monthly payments to retire the 30-year, $100,000 mortgage: about $119,500.

Again, you don't have to know how to figure how such things (although you could with a financial calculator and a little study). The key is to always be on guard against being overwhelmed by numbers.

This article first appeared in Kiplinger's Personal Finance magazine. For more help with your personal finances and investments, please subscribe to the magazine. It might be the best investment you ever make.